Published in PRR: Beating-free quantum oscillations in 2D gases with strong spin-orbit and Zeeman interactions
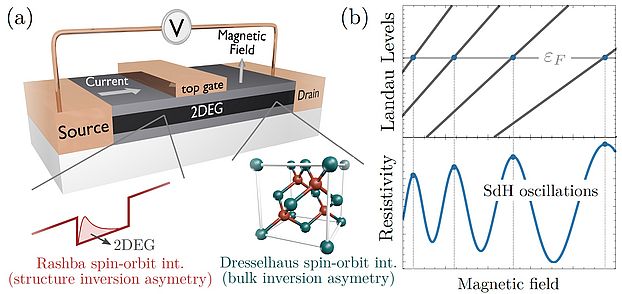
Shubnikov-de Haas (SdH) oscillations are the fingerprint of the Landau and Zeeman splitting level structure on the 2D resistivity, serving as a paradigmatic experimental probe. So far, no analytical description could be found for the vast majority of parameter space with Rashba, Dresselhaus and Zeeman terms present, usually relevant for experiments. Despite 50 years of experiments and many theoretical models, analysis and interpretation of experimental data was not so far easily accessible.
In this manuscript, we bridge this gap by providing an analytical formulation over a broad range of parameter space, using a Poisson summation formula for the density of states of the 2DEG. Further, we derive a simple condition for beating-free SdH oscillations a / b = [(1 - Delta ) / (1 + Delta )]1/2, with Delta ~ g*m* a material parameter given by the ratio of Zeeman and Landau energies, Rashba coefficient a and linear Dresselhaus parameter b. This condition is notably different from that of the persistent spin helix at a = b for materials with large g* m* such as InAs or InSb.
We also predict beatings in the higher harmonics of the SdH oscillations and elucidate the inequivalence of the SdH response of Rashba-dominated ( a > b ) vs Dresselhaus-dominated ( a < b ) 2DEGs in semiconductors with substantial g. We find excellent agreement with experimental data of Dettwiler et al. Phys. Rev. X 7, 031010 (2017), and Beukman et al., Phys. Rev. B 96, 241401 (2017).
The new formalism builds the foundation for a new generation of quantum transport experiments in quantum materials with unprecedented physical insight and material parameter extraction.
Beating-free quantum oscillations in 2D electron gases with strong spin-orbit and Zeeman interactions
Denis R. Candido, Sigurdur I. Erlingsson, Hamed Gramizadeh, Joao Vitor I. Costa, Pirmin J. Weigele, Dominik M. Zumbuhl, and J. Carlos Egues, Phys. Rev. Res. 5, 043297 (Dec 27, 2023), manuscript (incl. appendix) pdf
